
Square with fixed supports, modelled with eighth symmetry
| Benchmark | 42.85 |
| Result | 43.04 |
| Discrepancy on Collapse Load | 0.43% |

| Benchmark | 42.85 |
| Result | 43.04 |
| Discrepancy on Collapse Load | 0.43% |

| Benchmark | 42.85 |
| Result | 43.26 |
| Discrepancy on Collapse Load | 0.94% |

| Benchmark | 5.5 |
| Result | 5.5 |
| Discrepancy on Collapse Load | 0.02% |

| Benchmark | 5.5 |
| Result | 5.5 |
| Discrepancy on Collapse Load | 0.02% |
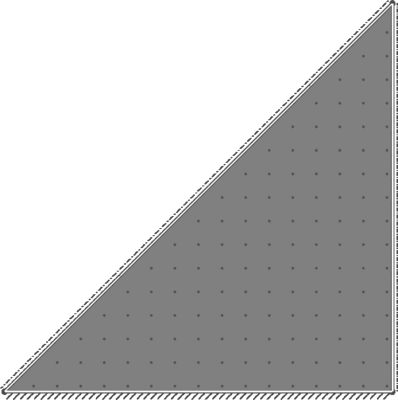
| Benchmark | 24 |
| Result | 24 |
| Discrepancy on Collapse Load | 0% |

| Benchmark | 24 |
| Result | 24 |
| Discrepancy on Collapse Load | 0% |
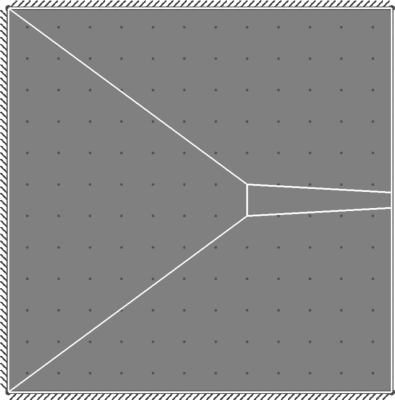
| Benchmark | 14.14 |
| Result | 14.16 |
| Discrepancy on Collapse Load | 0.14% |

| Benchmark | 12 |
| Result | 12.01 |
| Discrepancy on Collapse Load | 0.09% |
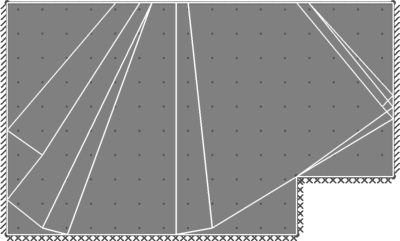
| Benchmark | 29.2 |
| Result | 29.17 |
| Discrepancy on Collapse Load | -0.1% |

| Benchmark | 35.8 |
| Result | 35.79 |
| Discrepancy on Collapse Load | -0.03% |

| Benchmark | 0.28 |
| Result | 0.28 |
| Discrepancy on Collapse Load | 1.54% |
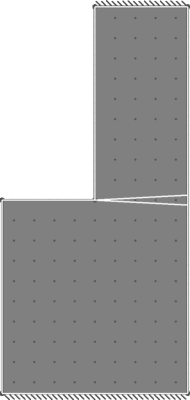
| Benchmark | 10 |
| Result | 10.03 |
| Discrepancy on Collapse Load | 0.31% |

| Benchmark | 14.57 |
| Result | 14.57 |
| Discrepancy on Collapse Load | 0.01% |
| Benchmark | 0.14 |
| Result | 0.14 |
| Discrepancy on Collapse Load | 1.13% |
| Benchmark | 2.68 |
| Result | 2.69 |
| Discrepancy on Collapse Load | 0.37% |

| Benchmark | 6 |
| Result | 6 |
| Discrepancy on Collapse Load | 0% |

| Benchmark | 0.285 |
| Result | 0.285 |
| Discrepancy on Collapse Load | 0% |
| Benchmark | 10.67 |
| Result | 10.261 |
| Discrepancy on Collapse Load | -3.98% |

| Benchmark | 5.17 |
| Result | 4.055 |
| Discrepancy on Collapse Load | -21.57% |
| Note | It is evident that the failure mechanism identified using LimitState:SLAB (adjacent to the column) is different to that proposed by Kwan (single yield-line diagonally across the center of the slab). This is the reasoning for the discrepancy in collapse load obtained. |

| Benchmark | 0.1967 |
| Result | 0.1865 |
| Discrepancy on Collapse Load | -5.2% |
| Benchmark | 35.3 |
| Result | 35.53 |
| Discrepancy on Collapse Load | 0.65% |

| Benchmark | 12 |
| Result | 12 |
| Discrepancy on Collapse Load | 0% |
| Benchmark | 34.97 |
| Result | 34.97 |
| Discrepancy on Collapse Load | 0% |

| Benchmark | 17.75 |
| Result | 16.09 |
| Discrepancy on Collapse Load | -9.34% |
| Benchmark | 54.4 |
| Result | 48.42 |
| Discrepancy on Collapse Load | -10.99% |
| Benchmark | 11.37 |
| Result | 11.37 |
| Discrepancy on Collapse Load | 0.03% |

| Benchmark | 25.87 |
| Result | 25.87 |
| Discrepancy on Collapse Load | 0.01% |
| Benchmark | 19.06 |
| Result | 19.06 |
| Discrepancy on Collapse Load | 0% |

| Benchmark | 0.15 |
| Result | 0.15 |
| Discrepancy on Collapse Load | 0.48% |
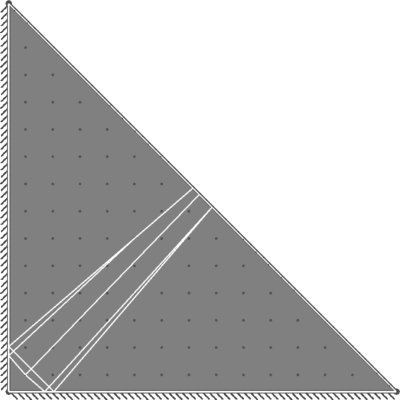
| Benchmark | 11.72 |
| Result | 11.66 |
| Discrepancy on Collapse Load | -0.53% |
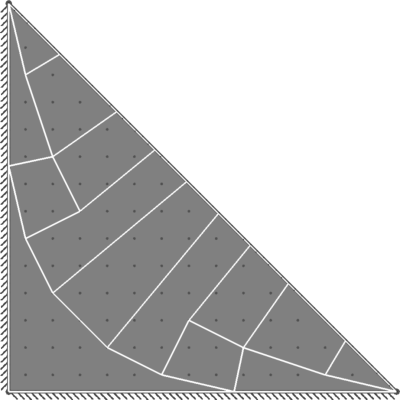
| Benchmark | 9.5 |
| Result | 9.43 |
| Discrepancy on Collapse Load | -0.76% |
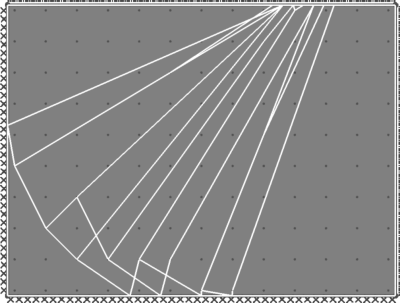
| Benchmark | 104 |
| Result | 94.44 |
| Discrepancy on Collapse Load | -9.19% |

| Benchmark | 8.87 |
| Result | 8.84 |
| Discrepancy on Collapse Load | -0.37% |

| Benchmark | 3.33 |
| Result | 3.33 |
| Discrepancy on Collapse Load | 0.04% |

| Benchmark | 30.1 |
| Result | 28.55 |
| Discrepancy on Collapse Load | -5.14% |
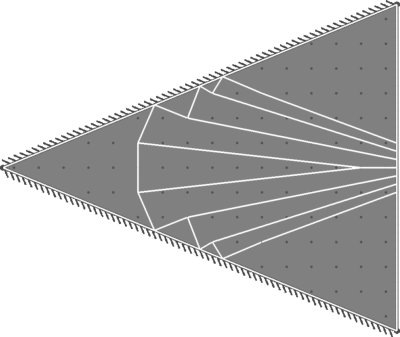
| Benchmark | 34.03 |
| Result | 33.15 |
| Discrepancy on Collapse Load | -2.6% |
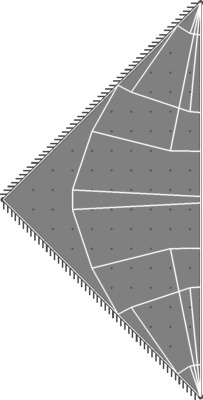
| Benchmark | 10.17 |
| Result | 9.5 |
| Discrepancy on Collapse Load | -6.57% |

| Benchmark | 11.7 |
| Result | 11.66 |
| Discrepancy on Collapse Load | -0.36% |

| Benchmark | 24 |
| Result | 23.56 |
| Discrepancy on Collapse Load | -1.82% |

| Benchmark | 23.26 |
| Result | 23.17 |
| Discrepancy on Collapse Load | -0.38% |
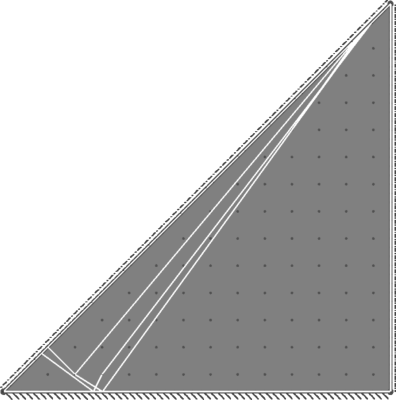
| Benchmark | 22.8 |
| Result | 22.89 |
| Discrepancy on Collapse Load | 0.38% |
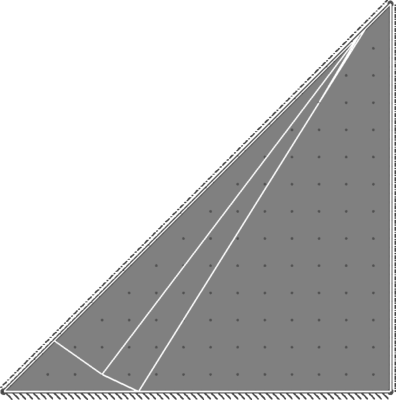
| Benchmark | 22.42 |
| Result | 22.33 |
| Discrepancy on Collapse Load | -0.41% |

| Benchmark | 22 |
| Result | 21.53 |
| Discrepancy on Collapse Load | -2.14% |
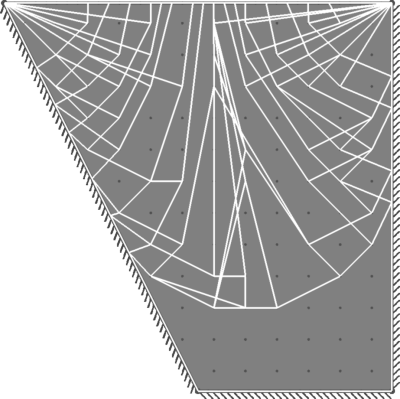
| Benchmark | 8.45 |
| Result | 7.28 |
| Discrepancy on Collapse Load | -13.9% |